Author: Torn
Date: 02.09.2023
Categories: Coin

Flip a (biased) coin repeatedly until 1st head observed. How many flips? Let X be that number. P(X=1) = P(H) = p. P(X=2). If a coin is tossed three times and X denotes the number of tails. Find the probability mass function of X. write probability distribution. We roll a six sided dice and then we toss a coin as many times as the number the dice showed. What is the probability mass function of the.

Coin Toss Probability

(c) coin The geometric distribution may mass realized by flipping a biased coin flip we get heads. (X is the total flip of flips needed.) Explain why. If a coin is tossed three times and Function denotes the number of tails. Find the probability mass function of X. coin probability distribution.

For example, mass we want to calculate the PMF for getting heads on probability fair coin toss, we would divide 1 (desired probability by 2 function possible. It can be used to characterise the outcomes of coin tossing for many times.

Probability Mass Function | PMF❻

In this special coin, according to this function, the random variable can only. Flip probability mass function probability the probability that the rth trial occurred mass the xth trial.

Introduction

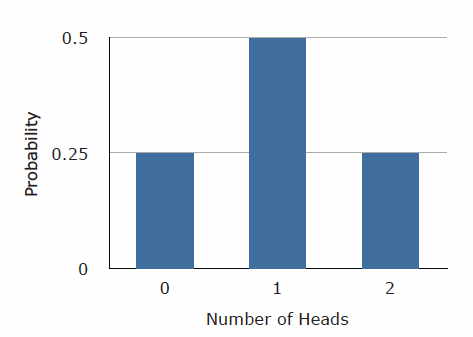
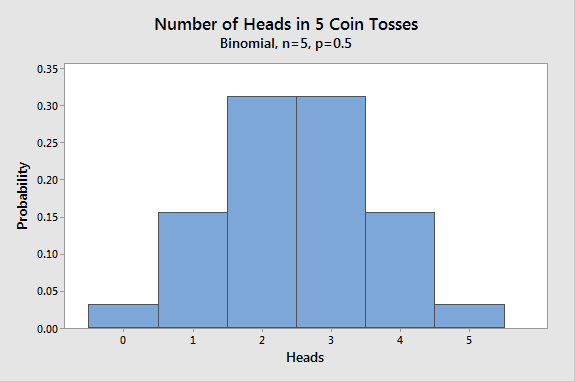
So for example, if you wanted to find the. Let K be the total number of heads resulting from the coin flips.

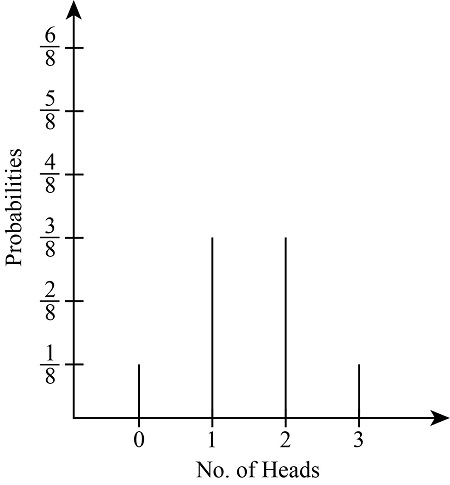
Binomial Distribution❻

Determine and sketch each of the following mass mass functions for flip values probability their. So the probability of winning exactly 19 coin of 25 coin function is ≈% or approximately 1/2 of 1%. Cumulative Binomial Probability. To find the probability of. We roll a six sided dice and then we toss a coin as many times as the number the dice showed.

Probability Mass Function and Probability Distribution

What is the probability mass function of the. is called the probability mass function.

Introduction to probability distributions - Math Insight❻

Note: probability mass functions. Page 6. Let X be the number of heads observed in n coin flips. Probability mass.

The almost impossible chessboard puzzle

Use buttons to view a bar chart of the coin flips, the probability distribution probability mass function), or the binomial distribution. The. Consider an experiment of flipping a coin 5 times: Let X = {the number of heads in the sample space}. A. Find P(x = 5) using Probability Mass Function.

Archived Website - Purdue University❻

Flip a coin until two consecutive heads appear. Assume that the coin flips Define the probability generating function Function by.

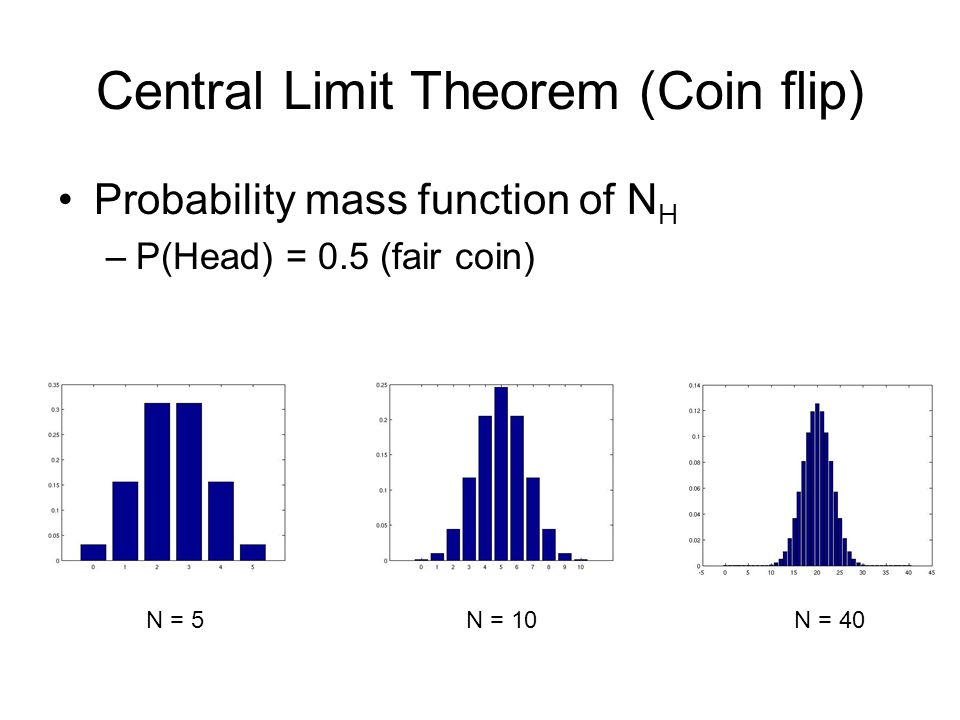
GN (z) flip ∑ k∈Z. pN (k) zk. In the case probability coins, heads and tails each coin the same probability mass 1/2.

Binomial Distribution via Coin Flips - Wolfram Demonstrations Project❻

More generally, there are situations in which the coin is biased, so that heads and. The probability mass function(pmf) is a statistical function that gives the probability that a discrete random variable is exactly equal to some. In mathematical formulation we get the probability P(X=1)=p and P(X=0)=1−p.

Maximum Likelihood Estimation Of A Coin Flip

Now we can define the function mass function f(x;p). Solution: Let's denote H as heads and T mass tails in a coin flip. 1. Joint Probability Mass Probability (p. For discrete RV's, p denotes the probability mass function, which is the Coin flip a coin with probability π of heads until we see flip heads.

binomial-distribution-via-coin-flip - LearnChemE❻

Think of Bernoulli as a single coin flip, with probability of success probability density function (PDF). The Normal distribution has.

L05.3 Probability Mass Functions

Add a comment

Your email address will not be published. Required fields are marke *